차밍이
[텐서플로/기초] 로지스틱 회귀 모델 구현으로 분류모델 만들기 실습 본문
텐서플로우 기초 실습하기 #3
이전 글에서는 단순 선형 회귀 모델을 바탕으로 regression 문제에 대해서 공부하였습니다. 이번 시간에는 로지스틱 회귀모델을 바탕으로 classification 모델을 만들어 보겠습니다.
이전 글
본 글에서는 텐서플로 1.15.0 버전을 사용하였습니다.
import tensorflow as tf
tf.__version__
>> 1.15.0로지스틱
로지스틱 회귀(logistic regression)는 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법입니다. 독립 변수의 선형 결합으로 종속변수를 설명하는 관점에서 선형 회귀 분석과 유사합니다. 하지만, 로지스틱 회귀 분석은 종속 변수가 범주형 데이터를 대상으로 하는 분류 문제를 다룹니다.
선형 회귀(Linear Regression) : regression 문제에 적용
로지스틱 회귀(Logistic Regression) : classification 문제에 적용
binary classification의 경우 0 or 1 또는 True or False 등의 이진분류의 문제입니다. 다항 로지스틱 회귀는 두 개 이상의 범주인 경우입니다.
로지스틱 함수 (logistic function):
로지스틱 함수의 그래프는 Figure 1과 같고 이는 독립 변수 x가 주어졌을 때 종속 변수가 1의 범주에 속할 확률을 의미한다. 즉, p(y = 1|x) 를 의미한다.
Logistic Regression 수식
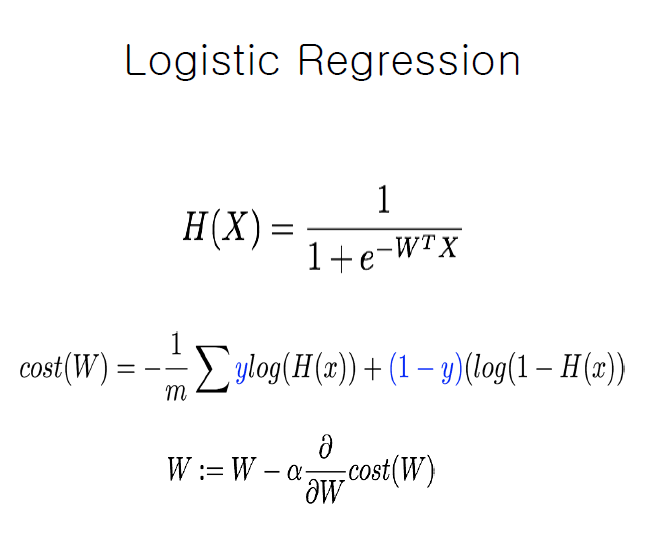
로지스틱 회귀 함수와 cost function은 위의 수식과 같이 나타낼 수 있습니다.
Source Code
암 관련 데이터 셋을 사용해서 16개의 feature들에 따른 암인지 또는 암이 아닌지를 분류하는 모델을 만들어보겠습니다.
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltpath = r"C:\Users\chan\Desktop\dataset"
df = pd.read_csv(path + "\ThoraricSurgery.csv", header=None)
df.head()| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 293 | 1 | 3.80 | 2.80 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 1 | 0 | 62 | 0 |
| 1 | 1 | 2 | 2.88 | 2.16 | 1 | 0 | 0 | 0 | 1 | 1 | 14 | 0 | 0 | 0 | 1 | 0 | 60 | 0 |
| 2 | 8 | 2 | 3.19 | 2.50 | 1 | 0 | 0 | 0 | 1 | 0 | 11 | 0 | 0 | 1 | 1 | 0 | 66 | 1 |
| 3 | 14 | 2 | 3.98 | 3.06 | 2 | 0 | 0 | 0 | 1 | 1 | 14 | 0 | 0 | 0 | 1 | 0 | 80 | 1 |
| 4 | 17 | 2 | 2.21 | 1.88 | 0 | 0 | 1 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 1 | 0 | 56 | 0 |
df.shape
>> (470, 18)StandardScaler를 사용해서 정규화를 해주었습니다. MinMaxScaler등 다른 scaler를 사용해도 무방합니다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
rdata = df.iloc[:,:-1]
data = scaler.fit_transform(rdata)
label = np.array(df.iloc[:,-1]).reshape(-1,1) # 행과 열을 조정 행렬 곱을 할 수 있게data.shape
>> (470, 17)텐서플로우를 활용해서 각 변수를 담기 위한 placeholder와 변수 W, b를 만들었습니다. 분류 모델이므로 sigmoid를 활성 함수로 사용하였습니다.
X = tf.placeholder(tf.float32, shape=[None,data.shape[1]])
Y = tf.placeholder(tf.float32, shape=[None,1])
W = tf.Variable(tf.random_normal([data.shape[1],1]))
b = tf.Variable(tf.random_normal([1]))
# 분류 모델에 따른 활성함수 sigmoid 사용
hf = tf.sigmoid(tf.matmul(X,W)+b)
# 로지스틱 회귀 모델의 cost function
cost = -tf.reduce_mean(Y*tf.log(hf) + (1-Y)*tf.log(1-hf))
opt = tf.train.GradientDescentOptimizer(0.001)
train = opt.minimize(cost)# 0.5를 기준으로 분류 기준을 나누었습니다.
predicted = tf.cast(hf>0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted,Y),dtype=tf.float32))# Session 만들기 & 초기화
sess = tf.Session()
sess.run(tf.global_variables_initializer())
feed_dict = {X:data, Y:label}# training 진행
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
feed_dict = {X:data, Y:label}
for step in range(20001):
_, cv = sess.run([train, cost], feed_dict=feed_dict)
if step % 1000 == 0:
print(f"cost : {cv}")
print("Training is Done")
print("=*="*10)
pv, hfv, av = sess.run([predicted, hf, accuracy],
feed_dict=feed_dict)
print(f"정확도 : {av}")
sess.close()cost : 0.9237145185470581
cost : 0.8028867244720459
cost : 0.7101439237594604
cost : 0.6389367580413818
cost : 0.5842043161392212
cost : 0.542082667350769
...
cost : 0.39898139238357544
cost : 0.39644089341163635
cost : 0.39425867795944214
cost : 0.39237144589424133
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8531914949417114Train_Test 나눠서 진행
Train과 Test 데이터를 나누어서 모델을 학습시키겠습니다. Train을 통해서 학습한 후, Test데이터를 통해서 검증하는 과정을 거치겠습니다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.3, random_state=33)
X = tf.placeholder(tf.float32, shape=[None,data.shape[1]])
Y = tf.placeholder(tf.float32, shape=[None,1])
W = tf.Variable(tf.random_normal([data.shape[1],1]))
b = tf.Variable(tf.random_normal([1]))
hf = tf.sigmoid(tf.matmul(X,W)+b)
cost = -tf.reduce_mean(Y*tf.log(hf) + (1-Y)*tf.log(1-hf))
opt = tf.train.GradientDescentOptimizer(0.001)
train = opt.minimize(cost)
predicted = tf.cast(hf>0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted,Y),dtype=tf.float32))with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
feed_dict = {X:X_train, Y:y_train}
for step in range(20001):
_, cv = sess.run([train, cost], feed_dict=feed_dict)
if step % 1000 == 0:
print(f"cost : {cv}")
print("Training is Done")
print("=*="*10)
pv, hfv, av = sess.run([predicted, hf, accuracy],
feed_dict={X:X_test,Y:y_test})
# print(f"예측값 : {pv}, \n 예측분류 : {hfv} \n, 정확도 : {av}")
print(f"정확도 : {av}")
sess.close()cost : 1.3811299800872803
cost : 1.2013882398605347
cost : 1.0589743852615356
cost : 0.9440013766288757
cost : 0.8495820760726929
cost : 0.770969569683075
...
cost : 0.4426581561565399
cost : 0.43336546421051025
cost : 0.4257008731365204
cost : 0.41939884424209595
cost : 0.41423311829566956
cost : 0.4100090563297272
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8510638475418091정확도가 거의 유사하게 나오는 것을 확인할 수 있습니다. 일반적인 경우는 아닌 것 같습니다.
분류 기준에 따른 변화 확인
분류 기준을 0.5를 기준으로 0 또는 1을 구분하였습니다. 이게 무슨 말이냐 하면, 암일 확률이 0.7이 나왔다고 가정하겠습니다. 암인지 아닌지를 구분하려는데 0.7만큼 암이다라는 결론은 뭔가 부족하겠죠? 그래서 분류하기 위한 기준으로 0.5를 둔 것입니다. 0.5 이상이면 암으로 분류하고 0.5 이하면 암이 아닌 것으로 분류하는 것입니다. 이러한 기준에는 명확하게 정해진 값은 없고 데이터셋마다 조금씩 다를 수 있다고 합니다.
분류기준을 바꿔가면서 어떤 값일 때, 가장 분류를 잘 하는지 확인해 보겠습니다.
accuracy_list = []
idx_list = []
for i in range(20,90,5):
idx = i/100
predicted = tf.cast(hf>idx, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted,Y),dtype=tf.float32))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(10001):
_, cv = sess.run([train, cost], feed_dict={X:X_train, Y:y_train})
print("Training is Done")
pv, hfv, av = sess.run([predicted, hf, accuracy],
feed_dict={X:X_test,Y:y_test})
print(f"정확도 : {av}")
print("=*="*10)
accuracy_list.append(av)
idx_list.append(idx)
sess.close()Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.6382978558540344
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.6241135001182556
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.716312050819397
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.7446808218955994
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.7730496525764465
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.7659574747085571
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8085106611251831
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8156028389930725
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8368794322013855
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8510638475418091
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8439716100692749
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8510638475418091
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8368794322013855
Training is Done
=*==*==*==*==*==*==*==*==*==*=
정확도 : 0.8439716100692749plt.plot(idx_list, accuracy_list)
기준이 낮을 때는 정확도가 매우 낮다가 점점 올라가는 것을 확인할 수 있습니다. 이후 0.85 근처에서 더 이상 증가하지 않습니다.
사실 텐서플로우를 실습하기 위해서 실습에 포커스를 맞추어서 데이터 자체를 잘 보지 않았습니다. 정확히 데이터 분석을 하기 위해서는 해당된 데이터를 자세히 살펴보아야 합니다. 위의 데이터의 경우는 데이터 불균형이 심해서 기본적으로 암이 아닌 경우가 훨씬 많습니다. 그래서 무조건 암이 아니라고 하면 80% 이상의 정답률을 가질 수 있습니다. 그러한 부분에서 문제가 있는 것 같습니다.
텐서 플로우 실습을 위한 부분이므로 여기에서 마치겠습니다.
지금까지 텐서 플로우를 사용해서 로지스틱 분류 모델을 직접 만들고 분류를 진행해보았습니다.
'파이썬 > Tensorflow & Keras' 카테고리의 다른 글
| [Keras] CNN ImageDataGenerator : 손글씨 글자 분류 (20) | 2020.05.05 |
|---|---|
| [Keras] CNN, 이미지 증식 : 손글씨 작성자 맞추기 (3) | 2020.05.04 |
| [Keras] CNN 이미지 분류 실습 : 손글씨 이미지 분류 (0) | 2020.04.29 |
| [텐서플로우/기초] 경사 하강법 구현 (0) | 2020.04.17 |
| [텐서플로우/기초] 단순 선형회귀 모델 및 손실함수 시각화 (0) | 2020.04.16 |





