차밍이
[텐서플로우/기초] 경사 하강법 구현 본문
텐서플로우 기초 실습하기 #2
목차
경사 하강법
경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다. [1] (출처 위키백과)
함수에서 주변부의 기울기가 가장 낮은 쪽으로 이동하는 방법입니다. 가장 경사가 급하게 감소하는 방향으로 움직인다고 생각하시면 됩니다. (주의할 점은 가장 낮은 값인 이유는 양의 값의 경우는 기울기가 커지는 값입니다.)
경사도, 기울기를 구하기 위해서는 미분이 필요합니다. 경사 하강법은 cost function(비용 함수)를 MSE 방식을 사용합니다. 아래와 같은 방식으로 표현하는 경우가 많습니다.

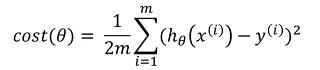
경사 하강법 수식

위 수식에서 알파는 학습률(Learning Rate)을 의미합니다. 미분을 통해서 기울기 값을 구하고 학습률 만큼 기존의 값에서 하강한 후, 이 값을 업데이트합니다.
경사 하강법 구현
텐서 플로우를 활용해서 옵티마이저들이 모두 구현되어 있으므로 굳이 구현할 필요는 없습니다. 하지만, 텐서플로우 연습 겸, 경사 하강법을 공부할 겸 한번 구현해보도록 하겠습니다.
# 데이터는 임의로 넣어서 사용하겠습니다.
xdata = [1,2,3]
ydata = [9,8,7]
w = tf.Variable(tf.random_normal([1]))
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
lr = 0.01
hf = x*w + b
cost = tf.reduce_mean(tf.square(hf-y))
gradient = tf.reduce_mean((w*x+b-y)*x) # Gradient :실제 갑소가 차이 후 x곱하기
descent = w-lr*gradient # learning rate만큼 gradient 값을 반영
update = w.assign(descent) # 텐서플로우에서는 assign 함수를 사용해야 값이 업데이트됨gradient, descent, update 세 가지 부분으로 나누어서 경사 하강법을 구현하였습니다.
모델 학습 진행
sess.run(tf.global_variables_initializer())
for step in range(21):
feed_dict = {x:xdata, y:ydata}
sess.run(update,feed_dict)
print(step, sess.run([cost,w],feed_dict))0 27.292152 [1.616255] [-0.8137552]
1 25.86602 [1.7104383] [-0.8137552]
2 24.583532 [1.8002262] [-0.8137552]
3 23.430946 [1.8858241] [-0.8137552]
4 22.395826 [1.9674274] [-0.8137552]
5 21.466875 [2.0452225] [-0.8137552]
6 20.633871 [2.1193871] [-0.8137552]
7 19.887537 [2.190091] [-0.8137552]
8 19.219477 [2.2574952] [-0.8137552]
9 18.622074 [2.3217537] [-0.8137552]
10 18.088434 [2.3830137] [-0.8137552]
11 17.612307 [2.4414148] [-0.8137552]
12 17.188044 [2.4970906] [-0.8137552]
13 16.810514 [2.550168] [-0.8137552]
14 16.475084 [2.6007686] [-0.8137552]
15 16.177559 [2.6490078] [-0.8137552]
16 15.914139 [2.6949959] [-0.8137552]
17 15.681393 [2.7388377] [-0.8137552]
18 15.476211 [2.7806337] [-0.8137552]
19 15.295784 [2.8204792] [-0.8137552]
20 15.137576 [2.8584652] [-0.8137552]각 step이 증가함에 따라서 cost값이 점점 줄어들고 weight와 bias값이 바뀌는 것을 확인할 수 있습니다. random state를 고정하지 않으면 매번 실행할 때마다 값이 달라질 수 있습니다. 처음에 임의의 지점을 시작되고 그 지점에서부터 점차 cost값을 줄이기 위한 방향으로 움직이게 됩니다.
추가 : weight값의 변화에 따른 cost 값의 변화 시각화
weight값에 변화를 주면서 cost가 낮아지는 방향으로 update가 된다는 것은 알고 있습니다. 그렇다면, weight값이 변화함에 따라서 cost가 어떻게 변화하는지 시각화 그래프를 그려서 확인해 보겠습니다.
import matplotlib.pyplot as plt
x = [1,3,5]
y = [10, 28, 40]
# weight : placeholder로 선언
w = tf.placeholder(tf.float32)
# b는 무시하고 w에 의한 변화만 확인
hf = x*w
loss = tf.reduce_mean(tf.square(hf-y))
w_history, c_history = [], []
for i in range(-100, 301, 1):
curr_w = i * 0.1
loss_v = sess.run(loss, {w:curr_w})
# weight의 갑소가 weight값에 따른 cost값 저장
w_history.append(curr_w)
c_history.append(loss_v)
plt.plot(w_history, c_history)
경사 하강법을 검색하면 흔히 볼 수 있는 그래프입니다. weight 값이 대략 8 정도의 값에서 가장 낮은 cost값을 보이는 것을 그래프를 통해서 볼 수 있습니다. 이와 같이 weight값이 점점 8에 가까운 숫자로 움직일 것임을 예상할 수 있겠습니다.
'파이썬 > Tensorflow & Keras' 카테고리의 다른 글
| [Keras] CNN ImageDataGenerator : 손글씨 글자 분류 (20) | 2020.05.05 |
|---|---|
| [Keras] CNN, 이미지 증식 : 손글씨 작성자 맞추기 (3) | 2020.05.04 |
| [Keras] CNN 이미지 분류 실습 : 손글씨 이미지 분류 (0) | 2020.04.29 |
| [텐서플로/기초] 로지스틱 회귀 모델 구현으로 분류모델 만들기 실습 (0) | 2020.04.18 |
| [텐서플로우/기초] 단순 선형회귀 모델 및 손실함수 시각화 (0) | 2020.04.16 |




