차밍이
[R] 선형회귀 모델과 상관관계를 통한 의료비 예측모델 : P-value와 R-squared 본문
미국 의료비 데이터를 활용해서 환자들의 의료비를 예측하는 모델을 만들어보겠습니다. 데이터는 케글에 있는 데이터를 활용했습니다.
데이터 확인
# 미국 환자 의료비 데이터
insurance<-read.csv("c:/rstudio_bc/Data/dataset_for_ml/insurance.csv")
str(insurance)
>>
# 'data.frame': 1338 obs. of 7 variables:
# $ age : int 19 18 28 33 32 31 46 37 37 60 ...
# $ sex : Factor w/ 2 levels "female","male": 1 2 2 2 2 1 1 1 2 1 ...
# $ bmi : num 27.9 33.8 33 22.7 28.9 25.7 33.4 27.7 29.8 25.8 ...
# $ children: int 0 1 3 0 0 0 1 3 2 0 ...
# $ smoker : Factor w/ 2 levels "no","yes": 2 1 1 1 1 1 1 1 1 1 ...
# $ region : Factor w/ 4 levels "northeast","northwest",..: 4 3 3 2 2 3 3 2 1 2 ...
# $ expenses: num 16885 1726 4449 21984 3867 ...나이, 성별, bmi 지수, 자식 수 , 흡연 여부, 지역 등의 정보를 가지고 있습니다. 이 데이터들을 통해서 expenses를 예측하면 되겠습니다.
선형 회귀 모델
-
선형 회귀 모델을 적용하기 위한 조건
일반적으로 선형 회귀 모델을 사용할 때에는 해당 데이터가 정규성을 따른다는 전제를 가지고 진행합니다. 꼭 정규분포를 따라야만 선형 회귀 모델을 쓸 수 있는 것은 아니지만, 정규분포를 따르면 선형 회귀 모델에 더 잘 맞아 들어갑니다. 그리고 선형성이 전혀 없는 경우는 모델이 잘 맞지 않는 경우가 많습니다.
-
선형성 확인
summary(insurance) >> # age sex bmi children smoker # Min. :18.00 female:662 Min. :16.00 Min. :0.000 no :1064 # 1st Qu.:27.00 male :676 1st Qu.:26.30 1st Qu.:0.000 yes: 274 # Median :39.00 Median :30.40 Median :1.000 # Mean :39.21 Mean :30.67 Mean :1.095 # 3rd Qu.:51.00 3rd Qu.:34.70 3rd Qu.:2.000 # Max. :64.00 Max. :53.10 Max. :5.000 # region expenses # northeast:324 Min. : 1122 # northwest:325 1st Qu.: 4740 # southeast:364 Median : 9382 # southwest:325 Mean :13270 # 3rd Qu.:16640 # Max. :63770 summary(insurance$expenses) # Min. 1st Qu. Median Mean 3rd Qu. Max. # 1122 4740 9382 13270 16640 63770 hist(insurance$expenses)

Histogram을 살펴보면 전반적으로 정규분포를 따른다고 보기에는 어렵습니다. 하지만 이정도면 사용할 수는 있을 것 같습니다.
상관관계
- 상관계수 확인
각 변수들 간의 상관 관계가 어떠한지 확인해보겠습니다. 성별, 흡연 여부, 지역은 factor 형태의 범주형 데이터 이므로 숫자형 데이터인 나이, bmi, chlidren, expenses의 상관관계를 확인해 보겠습니다.
check <- insurance[c("age","bmi",'children','expenses')]
cor(check)
>>
# age bmi children expenses
# age 1.0000000 0.10934101 0.04246900 0.29900819
# bmi 0.1093410 1.00000000 0.01264471 0.19857626
# children 0.0424690 0.01264471 1.00000000 0.06799823
# expenses 0.2990082 0.19857626 0.06799823 1.00000000expenses와 상관성을 보면 age와의 상관성이 그래도 가장 잘 나타나는 것 같습니다. bmi도 어느정도 양의 상관관계를 가직 ㅗ있습니다. children은 상관성이 있다고 보기는 어려울 것 같습니다.
- 그래프를 통한 시각화
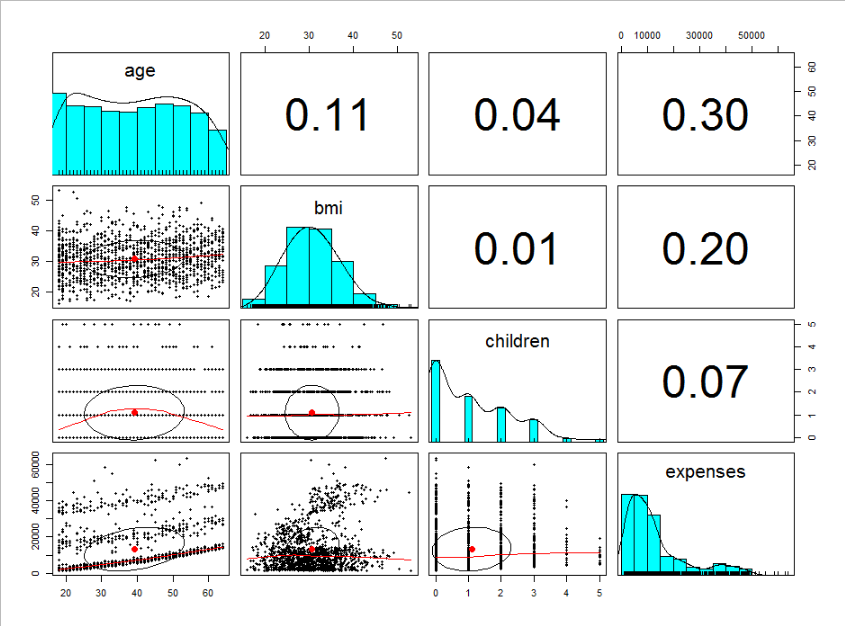
library(psych)
pairs.panels(check)그래프를 통해서 상관관계를 분석하면 더 좋습니다. psych 라이브러리를 활용하면 상관관계를 확인하는데 더 좋은 시각화를 할 수 있습니다.
선형 회귀 모델 생성
lm함수를 사용해서 모델을 생성해서 결과를 확인해 보겠습니다.
# 선형 회귀 모델 생성
ins_model <- lm(expenses~., data = insurance)
ins_model
summary(ins_model)
# Residuals: 오차
# Min 1Q Median 3Q Max
# -11302.7 -2850.9 -979.6 1383.9 29981.7
"
오차 최대가 3만정도 차이남 : 매우 큰 차이 발생
1사분위와 3사분위 사이의 값들이 대부분이므로
대부분의 오차가 저 사이의 값이라는 것
"
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -11941.6 987.8 -12.089 < 2e-16 ***
# age 256.8 11.9 21.586 < 2e-16 ***
# sexmale -131.3 332.9 -0.395 0.693255
# bmi 339.3 28.6 11.864 < 2e-16 ***
# children 475.7 137.8 3.452 0.000574 ***
# smokeryes 23847.5 413.1 57.723 < 2e-16 ***
# regionnorthwest -352.8 476.3 -0.741 0.458976
# regionsoutheast -1035.6 478.7 -2.163 0.030685 *
# regionsouthwest -959.3 477.9 -2.007 0.044921 *
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 6062 on 1329 degrees of freedom
# Multiple R-squared: 0.7509, Adjusted R-squared: 0.7494
# F-statistic: 500.9 on 8 and 1329 DF, p-value: < 2.2e-16최댓값과 최솟값이 매우 큰 차이를 보이는 것을 확인할 수 있습니다. 반면 1 사분위와 3 사분위 값의 차이는 상대적으로 덜한 편입니다. 대부분의 오차 값은 1 사분위와 3 사분위 사이에 있다고 생각하면 되겠습니다.
P-value
- P-value
- 위의 Coefficents들의
Pr(>|t|)에 해당하는 부분이 P-value의 값입니다. P-value 값이 작다는 것의 해당 상관관계가 흔하게 일어나는 일이 아니라는 것을 보여줍니다. - 쉽게 일어날 수 있는 값을 수록 P-value값이 커집니다. 작은만큼 쉽게 일어날 수 없는 확률을 의미합니다. 즉, P-value가 낮은 것은 해당 feature와의 상관관계혹은 선형 관계가 유의하다고 생각할 수 있습니다.
- 위의 출력 결과에 나와있는
***이러한 별 모양은 해당 P-value값이 얼마나 작은지에 따라서*의 갯수가 늘어납니다. 별의 개수가 많을수록 해당 feature와 종속변수와의 관계가 유의미한지를 나타냅니다.
- 위의 Coefficents들의
R-squared
- 회귀분석의 R-squared(결정계수)는 원자료에 대한 회귀선의 설명력을 의미합니다. 해당 모델에 회귀분석을 통한 선형성을 알고 있습니다. 그 모델이 종속변수(여기서의 expenses)를 얼마만큼 설명할 수 있는지를 의미합니다. R-squared 값을 통해서 해당 모델이 얼마만큼 설명력을 가지는 지를 확인하고, 만약 낮게 나왔다면 회귀선을 왜곡시키는 feature가 어떤 것인지 파악하는 데 사용하는 것이 좋겠습니다. 위의 결과에서 P-valure를 참고해서 유의미한 feature들만 사용하는 것도 좋은 생각입니다.
비선형성
-
모델이 선형적이라면 선형 관계가 잘 들어맞겠지만 사실 선형적인 관계가 아니므로 feature들을 조절해서 비선형성을 조절해줄 수 있습니다. 해당 feature의 P-value가 매우 높아 모델에 도움을 주지 못하는 경우 2가지 선택이 있습니다.
- 해당 feature를 삭제한다.
- feature들 간의 관계를 통해 새로운 feature를 만들어낸다.
- 수치형태의 자료를 이진화 또는 팩터화 하여 범주형 자료로 만들어 준다.
-
여기서 2번, 3번은 해당 분야 Domain에 대한 기본 지식이 있다면 더 좋을 것입니다. 예를 들어 bmi가 높고 담배를 피우는 사람의 경우 의료비가 많이 나갈 것이라는 생각을 할 수 있을 것입니다.
-
또는 나이와 비용간의 관계가 일차원 선형성 보다는 이차원 이상과의 선형성을 가질 것이라고 생각할 수도 있겠습니다.
-
위의 두 경우를 포함해서 모델을 새로 만들어 보겠습니다.
insurance$age2<-insurance$age^2 insurance$bmi_div<- ifelse(insurance$bmi>=30,1,0) ins_model.2<-lm(expenses~region+age2+age+children+bmi+sex+bmi_div*smoker ,data = insurance) summary(ins_model.2) >> Call: lm(formula = expenses ~ region + age2 + age + children + bmi + sex + bmi_div * smoker, data = insurance) Residuals: Min 1Q Median 3Q Max -17297.1 -1656.0 -1262.7 -727.8 24161.6 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 139.0053 1363.1359 0.102 0.918792 regionnorthwest -279.1661 349.2826 -0.799 0.424285 regionsoutheast -828.0345 351.6484 -2.355 0.018682 * regionsouthwest -1222.1619 350.5314 -3.487 0.000505 *** age2 3.7307 0.7463 4.999 6.54e-07 *** age -32.6181 59.8250 -0.545 0.585690 children 678.6017 105.8855 6.409 2.03e-10 *** bmi 119.7715 34.2796 3.494 0.000492 *** sexmale -496.7690 244.3713 -2.033 0.042267 * bmi_div -997.9355 422.9607 -2.359 0.018449 * smokeryes 13404.5952 439.9591 30.468 < 2e-16 *** bmi_div:smokeryes 19810.1534 604.6769 32.762 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 4445 on 1326 degrees of freedom Multiple R-squared: 0.8664, Adjusted R-squared: 0.8653 F-statistic: 781.7 on 11 and 1326 DF, p-value: < 2.2e-16bmi_div자체는 유의미 성이bmi보다 떨어졌지만bmi_div와smoker를 함께 섞어 주면서 아주 좋은 feature를 생성해냈습니다.age보다age2(나이의 제곱한 값)을 넣어주자age2가 더 좋은 결과를 나타내는 것을 확인할 수 있습니다.R-squared값이 0.75에서 0.86으로 설명력이 많이 개선된 것을 확인할 수 있습니다.
- R 공부하기
2020/02/04 - [R 프로그래밍] - [R프로그래밍] 실제 데이터를 사용한 데이터프레임과 그래프 활용
2020/02/06 - [R 프로그래밍] - [R] 연관 분석 Association analysis 과 Pruning
2020/02/19 - [R 프로그래밍] - [R] 딥러닝 neuralnet 라이브러리 활용 인공신경망 모델 생성 및 예측
'R > 데이터 사이언스' 카테고리의 다른 글
| [R] 딥러닝 neuralnet 라이브러리 활용 인공신경망 모델 생성 및 예측 (2) | 2020.02.19 |
|---|---|
| [R, kaggle실습] 영화 평점 감성 분석 - 텍스트 전처리에서 베이지안 필터기 적용까지 (0) | 2020.02.14 |
| [R] 나이브 베이즈를 활용한 스팸메일 분류와 텍스트 마이닝 (1) | 2020.02.11 |
| [R] 나이브 베이즈 분류(Naive Bayes Classifier) 활용 데이터 분석 및 실습 - 독버섯 분류하기 (2) | 2020.02.11 |
| [R] 머신러닝 - KNN을 사용한 암, 악성 종양 진단모델 (0) | 2020.02.06 |
| [R] 연관 분석 Association analysis 과 Pruning (0) | 2020.02.06 |
| [R프로그래밍] 실제 데이터를 사용한 데이터프레임과 그래프 활용 (0) | 2020.02.04 |



