차밍이
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 동적 계획법과 분할 정복 with 피보나치 본문
목차
1. 정의
동적계획법(Dynamic Programming)
- "DP"라고 많이 부름
- 큰 문제를 해결하기 위해, 작은 문제를 부분 부분 해결하여 저장해놓고 사용한다.
- 상향식 접근법으로 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결과를 이용해서 상위 문제를 해결한다.
- Memoization 기법을 사용한다.
- 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용된다.
- ex) 피보나치 수열
분할 정복(Divide and Conquer)
- 문제를 나눌 수 없을 때까지 나누어서 각각 문제를 풀면서 다시 합병하여 문제의 해답을 찾는다. 다시 합병한다.
- 하양식 접근법, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀 함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- ex) 병합 정렬, 퀵 정렬 등이 있다.
2. 공통점과 차이점
공통점
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할
차이점
- 동적 계획법
- 부분 문제는 중복되어 상위 문제에 다시 사용된다.
- Memoization 기법이 사용된다.
- 분할 정복
- 부분 문제는 서로 중복되지 않는다.
- Memo X
3. 동적 계획법 알고리즘 이해 - 피보나치
설명
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
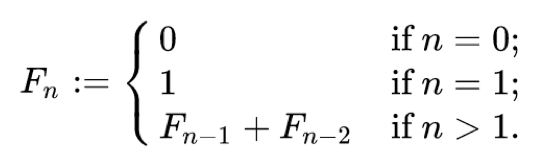
함수를 fibonacci 라고 하면,
fibonacci(0):0
fibonacci(1):1
fibonacci(2):1
fibonacci(3):2
fibonacci(4):3
fibonacci(5):5
fibonacci(6):8
fibonacci(7):13
fibonacci(8):21
fibonacci(9):34
DP를 사용해서 피보나치 문제를 해결해나가는 방법
피보나치 문제를 해결하기 위해서는 계속해서 작은 값들을 찾아 나가야 한다.

<간단 요약>
f(2) 값을 계속 계산하면 시간 낭비이므로 값을 저장한 후 필요할 때 바로 불러온다.
<상세하게>
f(6)의 값을 찾기 위해 f(4)의 값과 f(5)의 값을 계산해야 한다.
또 f(5)의 값을 찾기 위해서는 그 아래의 값을 찾아 나가야 한다.
이렇게 작은 부분으로 쪼개며 문제를 풀어나가는 부분에서는 "분할 정복"과 차이가 없다.
하지만, 위의 그림의 노란색 동그라미를 보자.
세부적으로 점점 파고들어 가면서 한번 계산한 값을 또다시 계산해야 한다.
f(2)의 값을 위의 사진에서 4번 잘린 부분까지 총 5번 필요하다.
매번 f(2)의 값을 계산하는 것은 시간 낭비이다.
따라서, 해당 함수를 계산하면 그 값을 저장해 두어(Memoization)한 후 나중에 해당 값이 필요하면 바로 사용하면 된다.
일반적인 피보나치
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
fibonacci(6)
>>> 8Memoization을 활용한 문제 풀이
storage = {}
def memo_fibonacci(n):
if n <= 1:
return n
elif n in storage:
return storage[n]
fibo_val = memo_fibonacci(n-1) + memo_fibonacci(n-2)
storage[n] = fibo_val
return fibo_val
memo_fibonacci(6)
>>> 8DP를 사용해서 피보나치를 풀기 위한 방법을 생각했다.
가장 중요한 Memoization을 사용해야 한다는 생각으로 문제를 처음 접근해서 풀었던 방식이다.
<설명>
일반적인 피보나치와 동일하지만 Memoization을 한 것이다.
storage 라는 dictionary를 만들어 해당 값이 계산되지 않은 경우 값을 계산해서 저장한다.
해당 값이 있으면 바로 꺼내서 사용한다.
But,
DP를 썼다고 보기는 부족하다.
최하위에서부터 상향식으로 문제를 풀었다고 보기 어렵다.
위의 문제를 풀기 위해 아래로 내려가면서 문제를 해결했고 해당 값을 찾기 위한 계산을 수행했다.
분할 정복에 가깝다고 생각되었다.
또한 함수 안에서 모든 것을 끝내지 못하고 외부 변수가 필요하다.
DP 활용한 문제 풀이
def dp_fib(n):
cache = [0 for i in range(n+1)]
cache[0], cache[1] = 0, 1
for i in range(2, n+1):
cache[i] = cache[i-1] + cache[i-2]
return cache[n]
dp_fib(6)
>>> 8<설명>
피보나치의 하위 값인 f(0)과 f(1) 값을 저장하고 이후 n 값을 1씩 높여가면서 원하는 n값의 피보나치를 찾아나간다.
함수 내에서 모든 것을 다 계산하고 마무리할 수 있다.
소요시간 비교

일반 피보나치 함수를 사용하면 n 값이 40만 되어도 한참 기다려도 끝나지 않는다.
memo_fibonacci 와 dp_fib를 비교해보면 거의 똑같은 시간이 걸리는 것을 볼 수 있다.
피보나치 n 값을 2000까지나 올렸음에도 거의 비슷한 시간 값을 보이고 있다.
확실한 것은 재귀 함수 방식의 피보나치 문제 풀이는 시간 측면에서 매우 비효율적임을 알 수 있다.
Reference - FastCampus 알고리즘-기술면접-완전정복 강의
이전 글 참고
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 삽입 정렬(Insertion Sort)
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 삽입 정렬(Insertion Sort)
목차 1. 삽입 정렬 방식 두 번째 인덱스에서부터 시작하여 데이터를 확인한다. 앞에 있는 데이터들과 하나씩 비교하면서 자신의 자리를 찾아나간다. 가장 작은 값이면 맨 앞까지 계속 이동한다.
chancoding.tistory.com
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 버블정렬
버블 정렬 두 인접한 원소를 검사하면서 정렬하는 방법 앞에서부터 두 개의 데이터를 비교하면서 정렬한다. 한 번 실행하면 가장 큰 값이 가장 뒤로 정렬되는 방식이다. 두 번째 실행하면 그다
chancoding.tistory.com
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 선택 정렬(Selection Sort)
[알고리즘] 패스트캠퍼스 알고리즘 학습 - 선택 정렬(Selection Sort)
1. 선택 정렬 이란? 주어진 데이터 중, 최솟값을 찾는다. 해당 최소값을 가장 맨 앞의 데이터의 위차와 교체한다. 맨 앞의 최소값 데이터를 제외한 나머지 데이터를 대상으로 동일한 방법을 반복
chancoding.tistory.com
'파이썬 > 알고리즘' 카테고리의 다른 글
| [Python] 백준 2164번 카드2 - deque (1) | 2021.07.25 |
|---|---|
| [파이썬] 백준 11047번 : 동전 0 - 알고리즘 문제풀이 (0) | 2021.06.26 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 - 병합 정렬(Merge Sort) (0) | 2021.04.12 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 - 퀵 정렬(Quick Sort) (0) | 2021.04.07 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 - 선택 정렬(Selection Sort) (0) | 2021.04.03 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 - 버블정렬 (0) | 2021.04.01 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 - 삽입 정렬(Insertion Sort) (0) | 2021.03.31 |
| [알고리즘] 패스트캠퍼스 알고리즘 학습 정리 - 더블 링크드 리스트(Double Linked List) (0) | 2021.02.09 |




